Image filtering with CUDA
and using shared memory
It can hardly be stressed enough how important it is to utilize shared memory when doing GPU computing. Shared memory allows us to re-arrange memory before writing, to take advantage of coalescing, and to re-use data to reduce the total number of global memory accesses.
In this exercise, you will start from a working CUDA program which applies a filter to an image. The original image is shown to the left, and the filtered image to the right, or, for wide images, the original above the result.
Your task is to accelerate this operation by preloading image data into shared memory. You will have to split the operation to a number of blocks and only read the part of the image that is relevant for your computation.
It can be noted that there are several ways to do image filtering that we do not take into account here. First of all, we can utilize separable filters. We may also use texture memory in order to take advantage of cache. Neither is demanded here. The focus here is memory addressing and local (shared) memory.
You need to use __shared__ for declaring shared memory, e.g. “__shared__ unsigned char[64];" for allocating a 64-byte array accessible to all threads in the block.
After loading data to shared memory, before processing, you should use __syncthreads() to synchronize. When running several kernels, use cudaDeviceSynchronize() to synchronize between the runs.
Lab files (updated 2022-12-07):
Old version just in case:
filter.cu is a naive CUDA implementation performs a simple convolution low-pass filter, not using shared memory. The files ppmread.c and ppmread.h are used to read and write PPM files (a very simple image format).
Tested in Olympen and Asgård:
nvcc filter.cu -c -arch=sm_30 -o filter.o
g++ filter.o milli.c readppm.c -lGL -lm -lcuda -lcudart -L/usr/local/cuda/lib -lglut -o filter
Three test images are included:
img1.ppm: 1280x640 photo by August Ernstsson. This is not exceptionally large but granted that we will present them at 1:1 on the screen we can consider it large.
baboon1.ppp: 512x512 photo of an ape, a common reference image.
maskros512.ppm: 512x512 photo that I snapped along a bike lane in Lambohov.

The same old dandelion that I always use. :)
Two of the images come with variants with added noise, intended for the median filter part: maskros-noisy.ppm and img1-noisy.ppm. The baboon is interesting for the median filter as is.
1. Make a low-pass box filter with shared memory
This is the biggest part of the lab! Once you have a working solution for this, the following steps should be fairly easy.
The low-pass filter that you have now is a straight-forward implementation with a very simple filter kernel, a flat, square kernel, a box filter. At this time, we will only care about the performance. With all pixels using pixels from a neighborhood, every pixel will be read multiple times. Your task is to accelerate this using shared memory! You need to support a filter size of at least 7x7 filters in order to get a significant speedup.
The convolution kernels below all have the origin in the center (except the 1x2 ones). They are symmetrical so we don’t have to worry about revering them properly for the convolution to be correct. The number in each box is the “tap”, the weight for the contribution of that particular neighbor.
Compare the performance of your optimized filter with the original version!
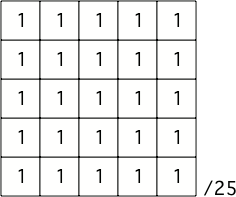
A 5x5 box filter
Notice the normalization in the corner. It is needed to make the filter give an output with the same magnitude as the input, which is simply the sum of the absolute of all kernel weights. This particular 5x5 filter requires a normalization scaling by 1/25.
Helpful hints:
• Each block should be responsible for the output to a specific output patch.
• Remember that a thread does not have to read in the same pixel that it will output! Simply giving each thread an amount of data to read to shared memory is both easy and efficient.
• The amount of work for each thread should be as balanced as possible.
• Don’t forget to plan for the border of the patch, the overlap between patches.
• There is no exactly correct result for pixels near the border of the image.
• There two input values kernelsizex and kernelsizey specify a filter with the size (kernelsizex*2+1) by (kernelsizey*2+1), that is kernelsizex and kernelsizey specify the radius beyond the center pixel, allowing only odd height and width. You should make sure that your solution supports non-symmetrical filters. There is also a maximum size, (maxKernelSizeX, maxKernelSizeY), which you should use when allocating shared memory since it can’t be controlled by dynamic input values.
We have modest expectations for your optimizations, but you should still produce a solid speedup compared to the naive version.
QUESTION: How much data did you put in shared memory?
QUESTION: How much data does each thread copy to shared memory?
QUESTION: How did you handle the necessary overlap between the blocks?
QUESTION: If we would like to increase the block size, about how big blocks would be safe to use in this case? Why?
QUESTION: How much speedup did you get over the naive version? For what filter size?
QUESTION: Is your access to global memory coalesced? What should you do to get that?
2. Separable LP filter
Two convolution kernels applied after each other on the same signal (image) will produce the same result as the convolution of the two kernels applied on the image. A common way to accelerate filters, not least LP filters like this, is to design separable filters, two or more filters that in combination will produce the desired filter, and since these filters are smaller, they may provide good optimizations. This is particularly true if we can split a 2D filter into two 1D filters,. Just like you did in Lab 3, we will try splitting the filter in two, one in each direction, still producing the same flat filter.
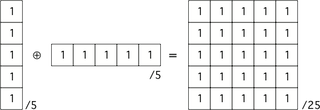
The convolution of an 1x5 and a 5x1 filter is a 5x5 filter
Your task: Rewrite the filter from step 1 to a separable filter and compare the result to the full NxN filter! Like before, larger sizes tend to show differences better. If your support for non-symmetrical filters is correct, it is mainly a matter of running the filter twice with different dimensions.
QUESTION: How much speedup did you get over the non-separated? For what filter size?
3. Convolution filters with kernel weights, gaussian filters
The box filter above is very simple and the result may result in visible blockiness caused by the shape of the filter. A better low-pass filter should be shaped more like a Gaussian filter. Here is a filter that approximates a Gaussian well enough to produce a much better result:
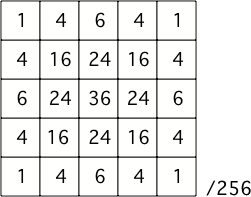
5x5 filter approximating a Gaussian
Conveniently, this filter is separable in two parts like this:
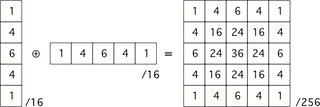
A separable 5x5 filter approximating a Gaussian kernel
Thus, we need 25 kernel weights for a 5x5 filter, or 5 each for the two passes of the separable filter.
However, separable filers don’t have to limit themselves to two passes. The particular filter above is separable in several steps, all the way down to eight 1x2 and 2x1 filters, like in the following figure:
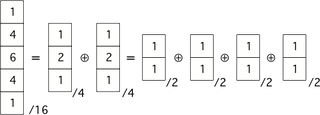
Separability of this filter can be taken to extremes!
Notice that I could break down this approximation to a Gaussian to a set of small box filters! There is a theorem for this, the central limit theorem, which states that repeated box filters will approximate a Gaussian blur!
Task: Implement the filter weights for a 1x5 / 5x1 filter.
QUESTION: Compare the visual result to that of the box filter. Is the image LP-filtered with the weighted kernel noticeably better?
QUESTION: What was the difference in time to a box filter of the same size (5x5)?
QUESTION: If you want to make a weighted kernel customizable by weights from the host, how would you deliver the weights to the GPU?
Other common convolution filters include gradient filters and Laplace filters, but we leave them for other courses.
4. Median filter
A median filter is a non-linear filter that returns the median of all pixel values in the neighborhood. It gives a certain blurring effect but its main usage is for noise reduction, since it preserves edges but suppresses noise.
As in lab 3, we process each channel independently.
Separable median filters
Since the median filter is non-linear, it is not possible to make a separable filter with the same result. However, a separable median filter is a good approximation of a median filter. You first take the median of a horizontal neighborhood. With the result of this first pass, you then take the median over a vertical neighborhood.
Task: Implement a median filter. It may be separable or non-separable. The size should be customizable by the parameters kernelsizex and kernelsizey. Test the filter both on the ordinary images and the noisy ones.
Non-mandatory: Implement both non-separable (exact) and separable (approximate) median filters.
QUESTION: What kind of algorithm did you implement for finding the median?
QUESTION: What filter size was best for reducing noise?
QUESTION (non-mandatory): Compare the result of the separable and full median filters.
QUESTION (non-mandatory): Compare the difference in performance of the separable and full median filters.
That was all for lab 5! Write down the answers to all questions and demonstrate for the assistant!
